Secret Sharing DAOs: The Different Crypto 2.0

The crypto 2.0 trade has been making robust progress up to now yr creating blockchain expertise, together with the formalization and in some instances realization of proof of stake designs like Slasher and DPOS, varied types of scalable blockchain algorithms, blockchains utilizing “leader-free consensus” mechanisms derived from conventional Byzantine fault tolerance principle, in addition to financial elements like Schelling consensus schemes and secure currencies. All of those applied sciences treatment key deficiencies of the blockchain design with respect to centralized servers: scalability knocks down dimension limits and transaction prices, leader-free consensus reduces many types of exploitability, stronger PoS consensus algorithms scale back consensus prices and enhance safety, and Schelling consensus permits blockchains to be “conscious” of real-world information. Nevertheless, there’s one piece of the puzzle that each one approaches up to now haven’t but managed to crack: privateness.

Foreign money, Dapps and Privateness

Bitcoin brings to its customers a slightly distinctive set of tradeoffs with respect to monetary privateness. Though Bitcoin does a considerably higher job than any system that got here earlier than it at defending the bodily identities behind every of its accounts – higher than fiat and banking infrastructure as a result of it requires no identification registration, and higher than money as a result of it may be mixed with Tor to utterly disguise bodily location, the presence of the Bitcoin blockchain implies that the precise transactions made by the accounts are extra public than ever – neither the US authorities, nor China, nor the 13 yr previous hacker down the road even want a lot as a warrant with a purpose to decide precisely which account despatched how a lot BTC to which vacation spot at what specific time. Normally, these two forces pull Bitcoin in reverse instructions, and it’s not totally clear which one dominates.

With Ethereum, the scenario is analogous in principle, however in follow it’s slightly completely different. Bitcoin is a blockchain supposed for forex, and forex is inherently a really fungible factor. There exist methods like merge avoidance which permit customers to basically faux to be 100 separate accounts, with their pockets managing the separation within the background. Coinjoin can be utilized to “combine” funds in a decentralized means, and centralized mixers are a superb choice too particularly if one chains lots of them collectively. Ethereum, however, is meant to retailer intermediate state of any form of processes or relationships, and sadly it’s the case that many processes or relationships which can be considerably extra complicated than cash are inherently “account-based”, and huge prices could be incurred by attempting to obfuscate one’s actions through a number of accounts. Therefore, Ethereum, because it stands at this time, will in lots of instances inherit the transparency aspect of blockchain expertise rather more so than the privateness aspect (though these enthusiastic about utilizing Ethereum for forex can actually construct higher-privacy money protocols within subcurrencies).

Now, the query is, what if there are instances the place individuals actually need privateness, however a Diaspora-style self-hosting-based resolution or a Zerocash-style zero-knowledge-proof technique is for no matter motive inconceivable – for instance, as a result of we need to carry out calculations that contain aggregating a number of customers’ personal information? Even when we clear up scalability and blockchain information property, will the dearth of privateness inherent to blockchains imply that we merely have to return to trusting centralized servers? Or can we give you a protocol that gives one of the best of each worlds: a blockchain-like system which provides decentralized management not simply over the precise to replace the state, however even over the precise to entry the knowledge in any respect?

Because it seems, such a system is effectively throughout the realm of chance, and was even conceptualized by Nick Szabo in 1998 beneath the moniker of “God protocols” (although, as Nick Szabo identified, we should always not use that time period for the protocols that we’re about to explain right here as God is usually assumed and even outlined to be Pareto-superior to the whole lot else and as we’ll quickly see these protocols are very removed from that); however now with the appearance of Bitcoin-style cryptoeconomic expertise the event of such a protocol might for the primary time truly be viable. What is that this protocol? To present it a fairly technically correct however nonetheless comprehensible time period, we’ll name it a “secret sharing DAO”.

Fundamentals: Secret Sharing

To skip the enjoyable technical particulars and go straight to purposes, click on right here

Secret computation networks depend on two basic primitives to retailer data in a decentralized means. The primary is secret sharing. Secret sharing basically permits information to be saved in a decentralized means throughout N events such that any Ok events can work collectively to reconstruct the information, however Ok-1 events can not get better any data in any respect. N and Ok will be set to any values desired; all it takes is a number of easy parameter tweaks within the algorithm.

The best option to mathematically describe secret sharing is as follows. We all know that two factors make a line:

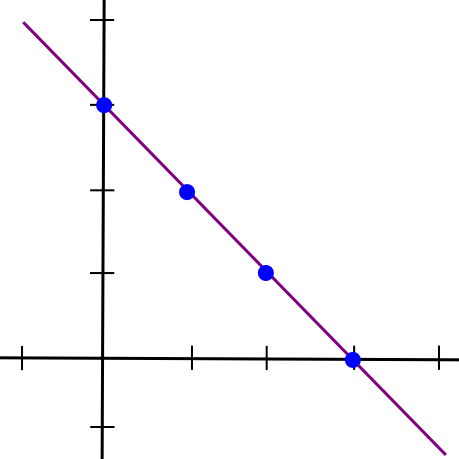
So, to implement 2-of-N secret sharing, we take our secret S, generate a random slope m, and create the road y = mx + S. We then give the N events the factors on the road (1, m + S), (2, 2m + S), (3, 3m + S), and many others. Any two of them can reconstruct the road and get better the unique secret, however one particular person can do nothing; in the event you obtain the purpose (4, 12), that might be from the road y = 2x + 4, or y = -10x + 52, or y = 305445x – 1221768. To implement 3-of-N secret sharing, we simply make a parabola as a substitute, and provides individuals factors on the parabola:

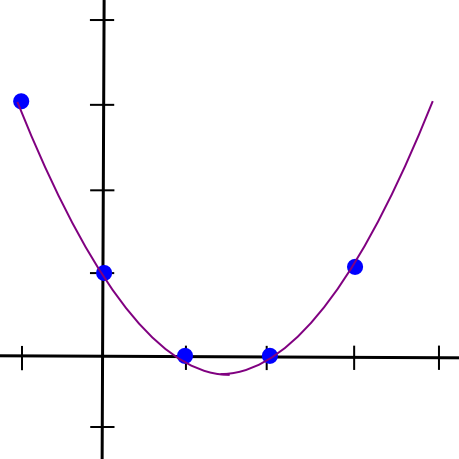
Parabolas have the property that any three factors on a parabola can be utilized to reconstruct the parabola (and nobody or two factors suffice), so basically the identical course of applies. And, extra typically, to implement Ok-of-N secret sharing, we use a level Ok-1 polynomial in the identical means. There’s a set of algorithms for recovering the polynomial from a ample set of factors in all such instances; they’re described in additional particulars in our earlier article on erasure coding.

That is how the key sharing DAO will retailer information. As a substitute of each collaborating node within the consensus storing a replica of the complete system state, each collaborating node within the consensus will retailer a set of shares of the state – factors on polynomials, one level on a special polynomial for every variable that makes up a part of the state.

Fundamentals: Computation

Now, how does the key sharing DAO do computation? For this, we use a set of algorithms referred to as safe multiparty computation (SMPC). The fundamental precept behind SMPC is that there exist methods to take information which is break up amongst N events utilizing secret sharing, carry out computations on it in a decentralized means, and find yourself with the end result secret-shared between the events, all with out ever reconstituting any of the information on a single machine.

SMPC with addition is straightforward. To see how, let’s return to the two-points-make-a-line instance, however now let’s have two traces:

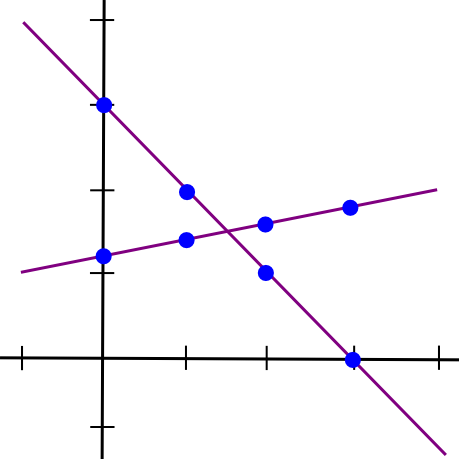
Suppose that the x=1 level of each traces A and B is saved by laptop P[1], the x=2 level is saved by laptop P[2], and many others. Now, suppose that P[1] computes a brand new worth, C(1) = A(1) + B(1), and B computes C(2) = A(2) + B(2). Now, let’s draw a line by way of these two factors:

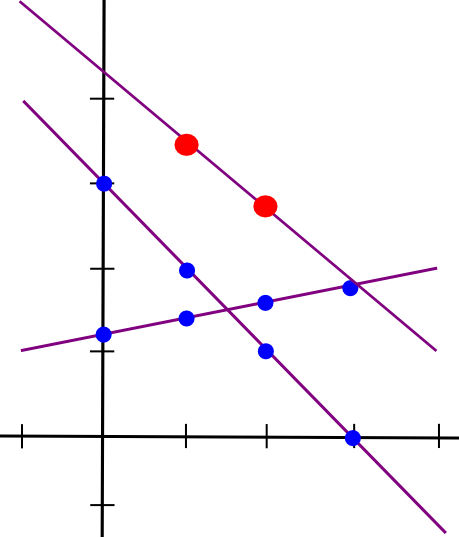
So now we have a brand new line, C, such that C = A + B at factors x=1 and x=2. Nevertheless, the attention-grabbing factor is, this new line is definitely equal to A + B on each level:

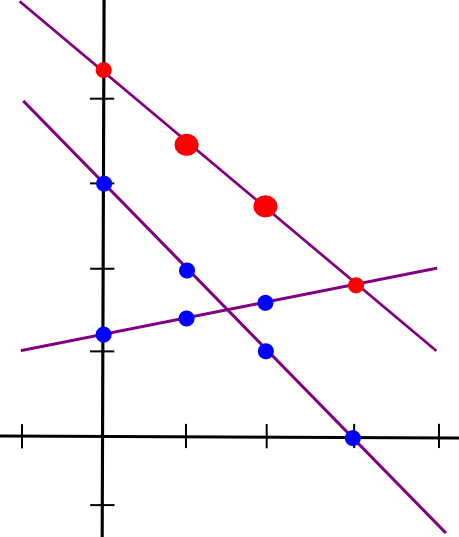
Thus, now we have a rule: sums of secret shares (on the similar x coordinate) are secret shares of the sum. Utilizing this precept (which additionally applies to greater dimensions), we are able to convert secret shares of a and secret shares of b into secret shares of a+b, all with out ever reconstituting a and b themselves. Multiplication by a identified fixed worth works the identical means: okay instances the ith secret share of a is the same as the ith secret share of a*okay.

Multiplication of two secret shared values, sadly, is rather more concerned. The strategy will take a number of steps to elucidate, and since it’s pretty sophisticated in any case it is value merely doing for arbitrary polynomials immediately. Here is the magic. First, suppose that there exist values a and b, secret shared amongst events P[1] … P[n], the place a[i] represents the ith share of a (and similar for b[i] and b). We begin off like this:

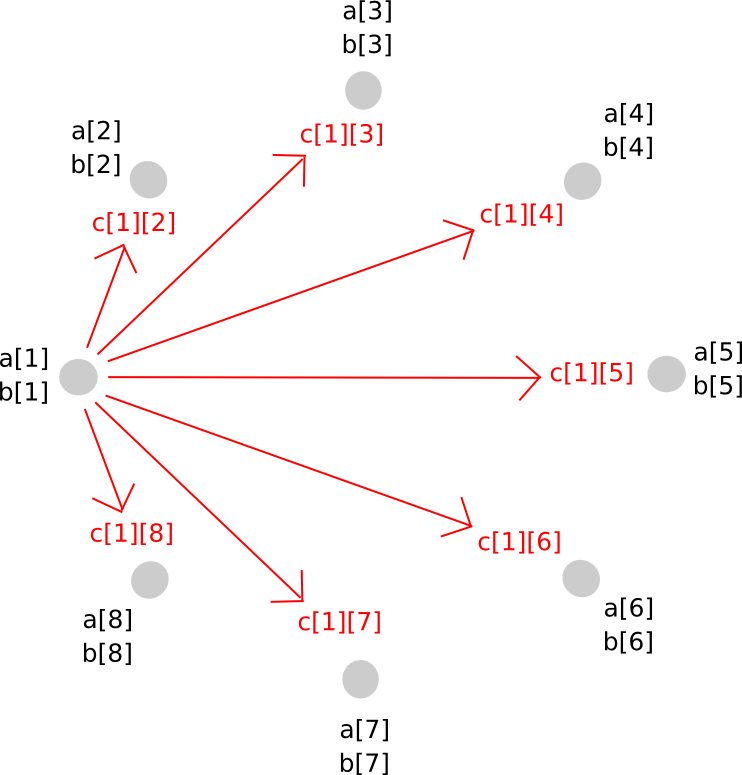
Now, one choice that you just would possibly consider is, if we are able to simply make a brand new polynomial c = a + b by having each get together retailer c[i] = a[i] + b[i], cannot we do the identical for multiplication as effectively? The reply is, surprisingly, sure, however with a significant issue: the brand new polynomial has a level twice as massive as the unique. For instance, if the unique polynomials had been y = x + 5 and y = 2x – 3, the product could be y = 2x^2 + 7x – 15. Therefore, if we do multiplication greater than as soon as, the polynomial would develop into too huge for the group of N to retailer.

To keep away from this downside, we carry out a kind of rebasing protocol the place we convert the shares of the bigger polynomial into shares of a polynomial of the unique diploma. The way in which it really works is as follows. First, get together P[i] generates a brand new random polynomial, of the identical diploma as a and b, which evaluates to c[i] = a[i]*b[i] at zero, and distributes factors alongside that polynomial (ie. shares of c[i]) to all events.

Thus, P[j] now has c[i][j] for all i. Given this, P[j] calculates c[j], and so everybody has secret shares of c, on a polynomial with the identical diploma as a and b.

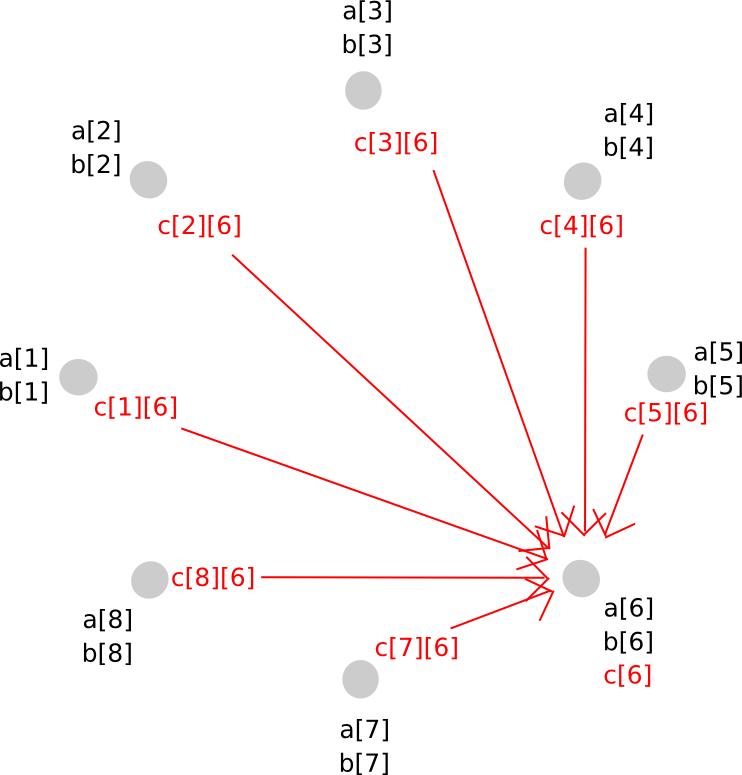
To do that, we used a intelligent trick of secret sharing: as a result of the key sharing math itself entails nothing greater than additions and multiplications by identified constants, the 2 layers of secret sharing are commutative: if we apply secret sharing layer A after which layer B, then we are able to take layer A off first and nonetheless be protected by layer B. This permits us to maneuver from a higher-degree polynomial to a decrease diploma polynomial however keep away from revealing the values within the center – as a substitute, the center step concerned each layers being utilized on the similar time.

With addition and multiplication over 0 and 1, now we have the power to run arbitrary circuits within the SMPC mechanism. We are able to outline:

• AND(a, b) = a * b
• OR(a, b) = a + b – a * b
• XOR(a, b) = a + b – 2 * a * b
• NOT(a) = 1 – a

Therefore, we are able to run no matter packages we wish, though with one key limitation: we won’t do secret conditional branching. That’s, if we had a computation if (x == 5) <do A> else <do B> then the nodes would wish to know whether or not they’re computing department A or department B, so we would wish to disclose x halfway by way of.

There are two methods round this downside. First, we are able to use multiplication as a “poor man’s if” – exchange one thing like if (x == 5) <y = 7> with y = (x == 5) * 7 + (x != 5) * y, utilizing both circuits or intelligent protocols that implement equality checking by way of repeated multiplication (eg. if we’re in a finite discipline we are able to test if a == b by utilizing Fermat’s little theorem on a-b). Second, as we’ll see, if we implement if statements contained in the EVM, and run the EVM inside SMPC, then we are able to resolve the issue, leaking solely the knowledge of what number of steps the EVM took earlier than computation exited (and if we actually care, we are able to scale back the knowledge leakage additional, eg. around the variety of steps to the closest energy of two, at some value to effectivity).

The key-sharing based mostly protocol described above is just one option to do comparatively merely SMPC; there are different approaches, and to realize safety there’s additionally a necessity so as to add a verifiable secret sharing layer on prime, however that’s past the scope of this text – the above description is just meant to indicate how a minimal implementation is feasible.

Constructing a Foreign money

Now that now we have a tough thought of how SMPC works, how would we use it to construct a decentralized forex engine? The final means {that a} blockchain is normally described on this weblog is as a system that maintains a state, S, accepts transactions, agrees on which transactions must be processed at a given time and computes a state transition operate APPLY(S, TX) -> S’ OR INVALID. Right here, we’ll say that all transactions are legitimate, and if a transaction TX is invalid then we merely have APPLY(S, TX) = S.

Now, because the blockchain isn’t clear, we would anticipate the necessity for 2 sorts of transactions that customers can ship into the SMPC: get requests, asking for some particular details about an account within the present state, and replace requests, containing transactions to use onto the state. We’ll implement the rule that every account can solely ask for stability and nonce details about itself, and might withdraw solely from itself. We outline the 2 forms of requests as follows:

SEND: [from_pubkey, from_id, to, value, nonce, sig]
GET: [from_pubkey, from_id, sig]

The database is saved among the many N nodes within the following format:

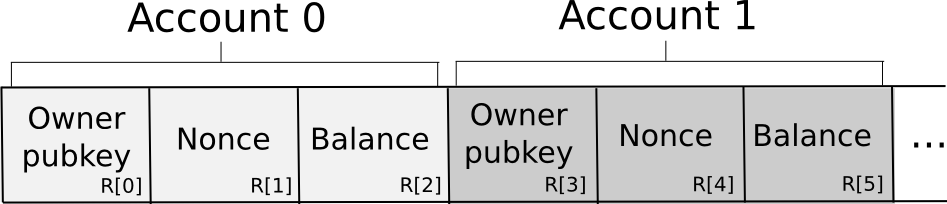
Basically, the database is saved as a set of 3-tuples representing accounts, the place every 3-tuple shops the proudly owning pubkey, nonce and stability. To ship a request, a node constructs the transaction, splits it off into secret shares, generates a random request ID and attaches the ID and a small quantity of proof of labor to every share. The proof of labor is there as a result of some anti-spam mechanism is critical, and since account balances are personal there is no such thing as a means if the sending account has sufficient funds to pay a transaction charge. The nodes then independently confirm the shares of the signature in opposition to the share of the general public key provided within the transaction (there are signature algorithms that help you do this type of per-share verification; Schnorr signatures are one main class). If a given node sees an invalid share (on account of proof of labor or the signature), it rejects it; in any other case, it accepts it.

Transactions which can be accepted aren’t processed instantly, very similar to in a blockchain structure; at first, they’re stored in a reminiscence pool. On the finish of each 12 seconds, we use some consensus algorithm – it might be one thing easy, like a random node from the N deciding as a dictator, or a complicated neo-BFT algorithm like that utilized by Pebble – to agree on which set of request IDs to course of and wherein order (for simplicity, easy alphabetical order will most likely suffice).

Now, to fufill a GET request, the SMPC will compute and reconstitute the output of the next computation:

owner_pubkey = R[0] * (from_id == 0) + R[3] * (from_id == 1) + ... + R[3*n] * (from_id == n)

legitimate = (owner_pubkey == from_pubkey)

output = legitimate * (R[2] * (from_id == 0) + R[5] * (from_id == 1) + ... + R[3n + 2] * (from_id == n))

So what does this system do? It consists of three phases. First, we extract the proprietor pubkey of the account that the request is attempting to get the stability of. As a result of the computation is completed within an SMPC, and so no node truly is aware of what database index to entry, we do that by merely taking all of the database indices, multiplying the irrelevant ones by zero and taking the sum. Then, we test if the request is attempting to get information from an account which is definitely owns (keep in mind that we checked the validity of from_pubkey in opposition to the signature in step one, so right here we simply must test the account ID in opposition to the from_pubkey). Lastly, we use the identical database getting primitive to get the stability, and multiply the stability by the validity to get the end result (ie. invalid requests return a stability of 0, legitimate ones return the precise stability).

Now, let’s take a look at the execution of a SEND. First, we compute the validity predicate, consisting of checking that (1) the general public key of the focused account is right, (2) the nonce is right, and (3) the account has sufficient funds to ship. Be aware that to do that we as soon as once more want to make use of the “multiply by an equality test and add” protocol, however for brevity we’ll abbreviate R[0] * (x == 0) + R[3] * (x == 1) + … with R[x * 3].

legitimate = (R[from_id * 3] == from_pubkey) * (R[from_id * 3 + 1] == nonce) * (R[from_id * 3 + 2] >= worth)

We then do:

R[from_id * 3 + 2] -= worth * legitimate
R[from_id * 3 + 1] += legitimate
R[to * 3 + 2] += worth * legitimate

For updating the database, R[x * 3] += y expands to the set of directions R[0] += y * (x == 0), R[3] += y * (x == 1) …. Be aware that each one of those will be parallelized. Additionally, word that to implement stability checking we used the >= operator. That is as soon as once more trivial utilizing boolean logic gates, however even when we use a finite discipline for effectivity there do exist some intelligent methods for performing the test utilizing nothing however additions and multiplications.

In all the above we noticed two basic limitations in effectivity within the SMPC structure. First, studying and writing to a database has an O(n) value as you just about need to learn and write each cell. Doing something much less would imply exposing to particular person nodes which subset of the database a learn or write was from, opening up the potential of statistical reminiscence leaks. Second, each multiplication requires a community message, so the basic bottleneck right here isn’t computation or reminiscence however latency. Due to this, we are able to already see that secret sharing networks are sadly not God protocols; they’ll do enterprise logic simply superb, however they may by no means be capable to do something extra sophisticated – even crypto verifications, excluding a choose few crypto verifications particularly tailor-made to the platform, are in lots of instances too costly.

From Foreign money to EVM

Now, the subsequent downside is, how can we go from this straightforward toy forex to a generic EVM processor? Properly, allow us to look at the code for the digital machine inside a single transaction setting. A simplified model of the operate appears to be like roughly as follows:

def run_evm(block, tx, msg, code):
    computer = 0
    gasoline = msg.gasoline
    stack = []
    stack_size = 0
    exit = 0
    whereas 1:
        op = code[pc]
        gasoline -= 1
        if gasoline < 0 or stack_size < get_stack_req(op):
            exit = 1
        if op == ADD:
            x = stack[stack_size]
            y = stack[stack_size - 1]
            stack[stack_size - 1] = x + y
            stack_size -= 1
        if op == SUB:
            x = stack[stack_size]
            y = stack[stack_size - 1]
            stack[stack_size - 1] = x - y
            stack_size -= 1
        ...
        if op == JUMP:
            computer = stack[stack_size]
            stack_size -= 1
        ...

The variables concerned are:

• The code
• The stack
• The reminiscence
• The account state
• This system counter

Therefore, we are able to merely retailer these as information, and for each computational step run a operate just like the next:

op = code[pc] * alive + 256 * (1 - alive)
gasoline -= 1

stack_p1[0] = 0
stack_p0[0] = 0
stack_n1[0] = stack[stack_size] + stack[stack_size - 1]
stack_sz[0] = stack_size - 1
new_pc[0] = computer + 1

stack_p1[1] = 0
stack_p0[1] = 0
stack_n1[1] = stack[stack_size] - stack[stack_size - 1]
stack_sz[1] = stack_size - 1
new_pc[1] = computer + 1
...
stack_p1[86] = 0
stack_p0[86] = 0
stack_n1[86] = stack[stack_size - 1]
stack_sz[86] = stack_size - 1
new_pc[86] = stack[stack_size]
...
stack_p1[256] = 0
stack_p0[256] = 0
stack_n1[256] = 0
stack_sz[256] = 0
new_pc[256] = 0

computer = new_pc[op]
stack[stack_size + 1] = stack_p1[op]
stack[stack_size] = stack_p0[op]
stack[stack_size - 1] = stack_n1[op]
stack_size = stack_sz[op]
computer = new_pc[op]
alive *= (gasoline < 0) * (stack_size < 0)

Basically, we compute the results of each single opcode in parallel, after which choose the right one to replace the state. The alive variable begins off at 1, and if the alive variable at any level switches to zero, then all operations from that time merely do nothing. This appears horrendously inefficient, and it’s, however bear in mind: the bottleneck isn’t computation time however latency. Every thing above will be parallelized. Actually, the astute reader might even discover that your complete technique of operating each opcode in parallel has solely O(n) complexity within the variety of opcodes (notably in the event you pre-grab the highest few gadgets of the stack into specified variables for enter in addition to output, which we didn’t do for brevity), so it’s not even essentially the most computationally intensive half (if there are extra accounts or storage slots than opcodes, which appears possible, the database updates are). On the finish of each N steps (or for even much less data leakage each energy of two of steps) we reconstitute the alive variable and if we see that alive = 0 then we halt.

In an EVM with many contributors, the database will possible be the most important overhead. To mitigate this downside, there are possible intelligent data leakage tradeoffs that may be made. For instance, we already know that more often than not code is learn from sequential database indices. Therefore, one strategy is perhaps to retailer the code as a sequence of huge numbers, every massive quantity encoding many opcodes, after which use bit decomposition protocols to learn off particular person opcodes from a quantity as soon as we load it. There are additionally possible some ways to make the digital machine basically rather more environment friendly; the above is supposed, as soon as once more, as a proof of idea to indicate how a secret sharing DAO is basically potential, not something near an optimum implementation. Moreover, we are able to look into architectures just like those utilized in scalability 2.0 methods to extremely compartmentalize the state to additional enhance effectivity.

Updating the N

The SMPC mechanism described above assumes an current N events concerned, and goals to be safe in opposition to any minority of them (or in some designs no less than any minority lower than 1/4 or 1/3) colluding. Nevertheless, blockchain protocols must theoretically final perpetually, and so stagnant financial units don’t work; slightly, we have to choose the consensus contributors utilizing some mechanism like proof of stake. To do that, an instance protocol would work as follows:

1. The key sharing DAO’s time is split into “epochs”, every maybe someplace between an hour and per week lengthy.
2. In the course of the first epoch, the contributors are set to be the highest N contributors through the genesis sale.
3. On the finish of an epoch, anybody has the power to enroll to be one of many contributors within the subsequent spherical by placing down a deposit. N contributors are randomly chosen, and revealed.
4. A “decentralized handoff protocol” is carried out, the place the N contributors concurrently break up their shares among the many new N, and every of the brand new N reconstitutes their share from the items that they acquired – basically, the very same protocol as was used for multiplication. Be aware that this protocol may also be used to extend or lower the variety of contributors.

All the above handles decentralization assuming trustworthy contributors; however in a cryptocurrency protocol we additionally want incentives. To perform that, we use a set of primitives referred to as verifiable secret sharing, that enable us to find out whether or not a given node was appearing actually all through the key sharing course of. Basically, this course of works by doing the key sharing math in parallel on two completely different ranges: utilizing integers, and utilizing elliptic curve factors (different constructions additionally exist, however as a result of cryptocurrency customers are most aware of the secp256k1 elliptic curve we’ll use that). Elliptic curve factors are handy as a result of they’ve a commutative and associative addition operator – in essence, they’re magic objects which will be added and subtracted very similar to numbers can. You possibly can convert a quantity into a degree, however not a degree right into a quantity, and now we have the property that number_to_point(A + B) = number_to_point(A) + number_to_point(B). By doing the key sharing math on the quantity stage and the elliptic curve level stage on the similar time, and publicizing the elliptic curve factors, it turns into potential to confirm malfeasance. For effectivity, we are able to most likely use a Schellingcoin-style protocol to permit nodes to punish different nodes which can be malfeasant.

Functions

So, what do now we have? If the blockchain is a decentralized laptop, a secret sharing DAO is a decentralized laptop with privateness. The key sharing DAO pays dearly for this further property: a community message is required per multiplication and per database entry. Because of this, gasoline prices are prone to be a lot greater than Ethereum correct, limiting the computation to solely comparatively easy enterprise logic, and barring using most sorts of cryptographic calculations. Scalability expertise could also be used to partially offset this weak spot, however finally there’s a restrict to how far you will get. Therefore, this expertise will most likely not be used for each use case; as a substitute, it should function extra like a special-purpose kernel that may solely be employed for particular sorts of decentralized purposes. Some examples embody:

• Medical information – retaining the information on a non-public decentralized platform can probably open the door for an easy-to-use and safe well being data system that retains sufferers answerable for their information. Significantly, word that proprietary analysis algorithms might run inside the key sharing DAO, permitting medical analysis as a service based mostly on information from separate medical checkup companies with out operating the danger that they may deliberately or unintentionally expose your personal particulars to insurers, advertisers or different companies.
• Personal key escrow – a decentralized M-of-N different to centralized password restoration; might be used for monetary or non-financial purposes
• Multisig for something – even methods that don’t natively assist arbitrary entry insurance policies, and even M-of-N multisignature entry, now will, since so long as they assist cryptography you’ll be able to stick the personal key within a secret sharing DAO.
• Fame methods – what if fame scores had been saved inside a secret sharing DAO so you could possibly privately assign fame to different customers, and have your project rely in the direction of the whole fame of that consumer, with out anybody having the ability to see your particular person assignments?
• Personal monetary methods – secret sharing DAOs might present an alternate path to Zerocash-style totally nameless forex, besides that right here the performance might be rather more simply prolonged to decentralized alternate and extra complicated sensible contracts. Enterprise customers might need to leverage among the advantages of operating their firm on prime of crypto with out essentially exposing each single one in all their inside enterprise processes to most of the people.
• Matchmaking algorithms – discover employers, workers, courting companions, drivers in your subsequent trip on Decentralized Uber, and many others, however doing the matchmaking algorithm computations within SMPC in order that nobody sees any details about you except the algorithm determines that you’re a excellent match.

Basically, one can consider SMPC as providing a set of instruments roughly just like that which it has been theorized could be provided by cryptographically safe code obfuscation, besides with one key distinction: it truly works on human-practical time scales.

Additional Penalties

Other than the purposes above, what else will secret sharing DAOs carry? Significantly, is there something to fret about? Because it seems, similar to with blockchains themselves, there are a number of issues. The primary, and most evident, difficulty is that secret sharing DAOs will considerably enhance the scope of purposes that may be carried out in a totally personal trend. Many advocates of blockchain expertise usually base a big a part of their argument on the important thing level that whereas blockchain-based currencies supply an unprecedented quantity of anonymity within the sense of not linking addresses to particular person identities, they’re on the similar time essentially the most public type of forex on the earth as a result of each transaction is situated on a shared ledger. Right here, nevertheless, the primary half stays, however the second half disappears utterly. What now we have left is actually complete anonymity.

If it seems to be the case that this stage of anonymity permits for a a lot greater diploma of legal exercise, and the general public isn’t proud of the tradeoff that the expertise brings, then we are able to predict that governments and different establishments normally, even perhaps alongside volunteer vigilante hackers, will attempt their finest to take these methods down, and maybe they’d even be justified. Fortuitously for these attackers, nevertheless, secret sharing DAOs do have an inevitable backdoor: the 51% assault. If 51% of the maintainers of a secret sharing DAO at some specific time determine to collude, then they’ll uncover any of the information that’s beneath their supervision. Moreover, this energy has no statute of limitations: if a set of entities who shaped over half of the sustaining set of a secret sharing DAO in some unspecified time in the future a few years in the past collude, then even then the group would be capable to unearth the knowledge from that time limit. Briefly, if society is overwhelmingly against one thing being completed within a secret sharing DAO, there shall be loads of alternative for the operators to collude to cease or reveal what is going on on.

A second, and subtler, difficulty is that the idea of secret sharing DAOs drives a stake by way of a cherished truth of cryptoeconomics: that personal keys aren’t securely tradeable. Many protocols explicitly, or implicitly, depend on this concept, together with non-outsourceable proof of labor puzzles, Vlad Zamfir and Pavel Kravchenko’s proof of custody, financial protocols that use personal keys as identities, any form of financial standing that goals to be untradeable, and many others. On-line voting methods usually have the requirement that it must be inconceivable to show that you just voted with a specific key, in order to forestall vote promoting; with secret sharing DAOs, the issue is that now you truly can promote your vote, slightly merely: by placing your personal key right into a contract within a secret sharing DAO, and renting out entry.

The results of this skill to promote personal keys are fairly far reaching – the truth is, they go as far as to virtually threaten the safety of the strongest out there system underlying blockchain safety: proof of stake. The potential concern is that this: proof of stake derives its safety from the truth that customers have safety deposits on the blockchain, and these deposits can probably be taken away if the consumer misacts in some trend (double-voting, voting for a fork, not voting in any respect, and many others). Right here, personal keys develop into tradeable, and so safety deposits develop into tradeable as effectively. We should ask the query: does this compromise proof of stake?

Fortuitously, the reply is not any. To start with, there are robust lemon-theoretic arguments for why nobody would truly need to promote their deposit. In case you have a deposit of $10, to you that is value $10 minus the tiny chance that you’re going to get hacked. However in the event you attempt to promote that deposit to another person, they may have a deposit which is value $10, except you determine to make use of your personal key to double-vote and thus destroy the deposit. Therefore, from their standpoint, there’s a fixed overhanging threat that you’ll act to take their deposit away, and also you personally haven’t any incentive not to try this. The actual fact that you’re attempting to dump your deposit ought to make them suspicious. Therefore, from their standpoint, your deposit would possibly solely be value, say, $8. You haven’t any motive to sacrifice $10 for $8, in order a rational actor you’ll hold the deposit to your self.

Second, if the personal key was within the secret sharing DAO proper from the beginning, then by transferring entry to the important thing you’ll personally lose entry to it, so you’ll truly switch the authority and the legal responsibility on the similar time – from an financial standpoint, the impact on the system could be precisely the identical as if one of many deposit holders merely had a change of character in some unspecified time in the future through the course of. Actually, secret sharing DAOs might even enhance proof of stake, by offering a safer platform for customers to take part in decentralized stake swimming pools even in protocols like Tendermint, which don’t natively assist such performance.

There are additionally different explanation why the theoretical assaults that secret sharing DAOs make potential might the truth is fail in follow. To take one instance, take into account the case of non-outsourceable puzzles, computational issues which attempt to show possession of a non-public key and a bit of knowledge on the similar time. One form of implementation of a non-outsourceable puzzle, utilized by Permacoin, entails a computation which must “bounce” backwards and forwards between the important thing and the information tons of of hundreds of instances. That is simple to do when you’ve got the 2 items of knowledge on the identical piece of {hardware}, however turns into prohibitively gradual if the 2 are separated by a community connection – and over a secret sharing DAO it might be almost inconceivable because of the inefficiencies. Because of this, one potential conclusion of all that is that secret sharing DAOs will result in the standardization of a signature scheme which requires a number of hundred tens of millions of rounds of computation – ideally with heaps and many serial multiplication – to compute, at which level each laptop, telephone or internet-of-things microchip would have a built-in ASIC to do it trivially, secret sharing DAOs could be left within the mud, and we might all transfer on with our lives.

How Far Away?

So what’s left earlier than secret sharing DAO expertise can go mainstream? Briefly, fairly a bit, however not an excessive amount of. At first, there’s actually a average quantity of technical engineering concerned, no less than on the protocol stage. Somebody must formalize an SMPC implementation, along with how it might be mixed with an EVM implementation, most likely with many restrictions for effectivity (eg. hash features within SMPC are very costly, so Merkle tree storage might disappear in favor of each contract having a finite variety of storage slots), a punishment, incentive and consensus framework and a hypercube-style scalability framework, after which launch the protocol specification. From that time, it is a number of months of improvement in Python (Python must be superb, as by far the first bottleneck shall be community latency, not computation), and we’ll have a working proof of idea.

Secret sharing and SMPC expertise has been on the market for a few years, and tutorial cryptographers have been speaking about tips on how to construct privacy-preserving purposes utilizing M-of-N-based primitives and associated applied sciences equivalent to personal data retrieval for over a decade. The important thing contribution made by Bitcoin, nevertheless, is the concept that M-of-N frameworks normally will be rather more simply bootstrapped if we add in an financial layer. A secret sharing DAO with a forex inbuilt would supply incentives for people to take part in sustaining the community, and would bootstrap it till the purpose the place it might be totally self-sustaining on inside purposes. Thus, altogether, this expertise is sort of potential, and never almost so far-off; it is just a matter of time till somebody does it.

Supply hyperlink

from Ethereum – My Blog https://ift.tt/DLPEOqT
via IFTTT